前言
书接上回,本章节为下篇:TileMatrixSet实现及相关计算原理探讨。
本章节将以TileMatrixSet模型的典型实现,即GeoWebCache中的Gridset作为开端,对OGC中TileMatrxSet模型进行印证。而后对TileMatrixSet相关计算原理进行探讨,并以CGCS2000切片方案为例进行验证。另附带说明TileMatrixSet在Geo Atlas中的实现及应用 🤨。
Gridset & TileMatrixSet
这里就不再对GeoWebCache做介绍了,直接切入主题。GeoWebCache中的Gridset正是对应着TileMatrixSet模型,我们先来看一下GeoWebCache对于Gridset的相关介绍:
Gridsets and Gridsubsets
Gridsets 和 Gridsubsets 是指 GeoWebCache 所服务的图层的空间参考系统(the spatial reference system)。从本质上来说,正如 Tiles 中所介绍的,GeoWebCache 与参考系统无关。当 GeoWebCache 向 WMS 发出请求时,它使用 Gridsets 和 Gridsubsets 信息将其内部切片索引转换为 WMS 可以理解的空间请求。
💡 说实话,有时候我觉得老外的啰嗦话挺多的,其实这里就是表达GeoWebCache就是使用 Gridsets 和 Gridsubsets 将瓦片坐标转换为瓦片对应的空间范围的。从其实现来看,此处所述的内部切片索引正是对应着瓦片坐标系。
下面分别对 Gridset 和 Gridsubset 的构成进行描述,此处引用原文:
A gridset is a global definition (i.e. not layer-specific) specifying:
全局定义即对应着通用的切片方案,所以不是特定于层(图层)的。
-
A spatial reference system (EPSG code)
对应着投影坐标系。
-
A bounding box describing the extent, typically the maximum extent for the above reference system
描述范围的边界框,通常是上述参考系统的最大范围(也就是说,也可以是你自行定义)
-
One of either a list of scale denominators, resolutions, or zoom levels
比例分母、分辨率或缩放级别列表之一。(对应着尺度分级)
-
The tile dimensions in pixels (constant for all zoom levels)
以像素为单位的瓦片尺寸(对于所有缩放级别均保持不变)。
💡 这也是我在前文说的,目前大部分情况下,瓦片的尺寸基本都使用像素作为单位进行换算。同时,OGC TileMatrixSet中提出的是每个维度(尺度层级)下瓦片大小要一致,但是不同维度的瓦片大小可以不一致。不过在GeoWebCache实现中,要求全维度都使用相同的瓦片大小。当然,这也符合实际中绝大部分的使用情况。
-
(Optional) Pixel size (to calculate scales). The default is 0.28mm/pixel, corresponding to 90.71428571428572 DPI.
(可选)像素大小(用于计算比例)。默认为0.28mm/像素,对应90.71428571428572 DPI。
💡 这里的Pixel Size对应着Cell Size,其以米为单位。 而0.28mm的来源,前文也曾提到:通常,设备的真实像素尺寸是未知的,0.28 毫米是 2005 年普通显示器的实际像素尺寸。即使当前的显示设备采用小得多的像素尺寸,该值仍被用作参考。 注:自 20 世纪 80 年代以来,Microsoft Windows 操作系统已将其默认的标准显示每英寸像素 (PPI) 设置为 96。该值的结果约为每像素 0.264 mm。该值与本标准中采用的实际 0.28mm 的相似性可能会造成一些混乱。
对于90.71428571428572数值来源,可继续往下看,切片原理部分会做解释。
A gridsubset is a layer-specific definition specifying:
gridsubset 是特定于图层的,这是因为其代表着数据的真实范围。(对应着TileMatrixSet Limits)
💡 从GeoServer的实现中,图层的BBox是在发布时从数据源处获取的,该图层数据的BBox即为gridsubset的边界范围
-
The gridset for the layer
其实,Gridset 和 Gridsubset 通常是成对出现的,若有子集则必有原集,但Gridset是可以单独存在的。这两是在同一投影坐标系下,相同尺度分级下、不同BBox(BBox的关系是包含与被包含的关系)的TileMatrixSet实现,只不过 Gridsubset 基本作为辅助元素。
-
(Optional) The bounding box for that layer (which must be a subset of the extent of the gridSet)
(可选)该层的边界框(必须是gridSet范围的子集)
💡 可选就很灵性,也就是说也可以取默认,也就是取投影坐标系的范围。
-
(Optional) A list of zoom levels (which must be a subset of what is defined in the gridSet)
(可选)缩放级别列表(必须是 gridSet 中定义的子集)
💡 此处描述的不是可以自定义尺度分级,而是在 GridSet定义的基础上的限定。比如GridSet中定义了0-23级,那么subset只能是0-23的子集,可以限定,但是不可以再行定义。
By default, this information is set in geowebcache.xml.
💡 从上文的描述中,并没有提及切片原点相关的内容。从其实现可知,其默认使用左下角作为切片原点进行实现的,这也是OGC的提倡。那为什么不在此处做出明示呢?估计是遵从约定大于配置原则 也未可知啊!(裘千丈警告😂)
From gridsets to tiles
以下是解释在特定缩放级别下的网格集和子网格集的构建过程,并确定正在请求(可以请求)哪些瓦片。(这句翻译烫嘴🙄)

对于上述介绍来说,我们现阶段只需要留意以下几个地方就好,像比例和范围计算可暂不用完全理解。
-
对于Gridset,给定的边界不一定是Gridset中各格网域的最终边界,应该还需要根据规则进行计算,给定的边界不一定可以正好适合,所以会存在拓展的情况。Gridsubset同理。这也与上文中关于TileMatrixSet域部分对应:每个瓦片矩阵集都有一个可选的近似边界框(即BBox,之所以近似应是因为一般取是最小外接矩形MBR →Minimum Bounding Rectangle,并非完全一致。Maybe🤔),但每个瓦片矩阵都有一个精确的边界框,该边界框是从其他参数间接推导出来的。由于单元格对齐方式不同,每个比例下的瓦片矩阵边界框通常会略有不同(比如4490经纬度投影的0级和1级的边界框就不同)。
-
上述内容提到,默认是将边界框对齐到左下角。也就是说,默认情况下,是使用左下角作为切片原点,但是可以通过
进行设置是否与右上角对其。 注:此为GeoWebCache的默认配置(左下角)。 切片原点不同,那么瓦片坐标也不同,但是可以进行相互转换。
-
Gridsubset就是限制,只有处于Gridsubset范围内的切片,才允许被访问
💡 对于上述内容中给出的Gridset的BBox与Gridsubset的BBox的数值可不用过多理会,只要明白图示表达的意思就行。
Gridset 实现
这里只贴GridSet和Grid的属性部分代码
GridSet
public class GridSet implements Info {
private String name;
private SRS srs;
// 瓦片宽度,一般为256,像素单位
private int tileWidth;
// 瓦片高度,一般为256,像素单位
private int tileHeight;
/**
* Whether the y-coordinate of {@link #tileOrigin()} is at the top (true) or at the bottom
* (false)
*/
protected boolean yBaseToggle = false;
/**
* By default the coordinates are {x,y}, this flag reverses the output for WMTS getcapabilities
*/
private boolean yCoordinateFirst = false;
private boolean scaleWarning = false;
private double metersPerUnit;
private double pixelSize;
// 限定的格网边界
private BoundingBox originalExtent;
private Grid[] gridLevels;
private String description;
/**
* {@code true} if the resolutions are preserved and the scaleDenominators calculated, {@code
* false} if the resolutions are calculated based on the sacale denominators.
*/
private boolean resolutionsPreserved;
}
Grid
public class Grid implements Serializable, Cloneable {
private static final long serialVersionUID = 1L;
// 矩阵宽度,即横向的瓦片数量
private long numTilesWide;
// 矩阵高度,即纵向的瓦片数量
private long numTilesHigh;
// 分辨率
private double resolution;
// 比例分母
private double scaleDenom;
private String name;
}
对比OGC TileMatrixSet UML Model可以发现,GridSet并非完全遵循OGC的标准实现,可以在其基础上进行了一定的修改。当然,这和我目前看的TileMatrixSet标准的版本也有关系(比如说:cornerOfOrigin)。
- GridSet中要求所有层级的瓦片尺寸大小不变,所以将Grid中的tileWidth、tileHeight、pixelSize提升到GridSet中定义。
- 命名基本不一致
- 部分简化,又做了一定拓展。比如CRS 变更为SRS,但是兼容别名访问(3857,900913);比如同时支持比例分母和分辨率来进行尺度分级定义,两者可以相互转换。
💡 其实,我也觉得标准给得相对复杂了些。在各自的场景下可以进行简化,甚至部分内容固定化。
切片原理
术语
-
DPI(英语:Dots Per Inch,每英寸点数):是一个量度单位,用于点阵数字图像,意思是指每一英寸长度中,取样或可显示或输出点的数目。如:打印机输出可达300DPI的分辨率,表示打印机可以每一平方英寸的面积中可以输出300x300=90000个输出点。
打印机所设置之分辨率的DPI值越高,印出的图像会越精细。打印机通常可以调校分辨率。例如撞针打印机,分辨率通常是60至90 DPI。喷墨打印机则可达300~720 DPI。激光打印机则有600~1200 DPI。
一般显示器为96 DPI,印刷所需位图的DPI数则视印刷网线数(lpi)而定。一般150线印刷质量需要350 DPI的位图。而这里的D(dot)就是像素(pixel)。
-
PPI:每英寸像素(英语:Pixels Per Inch,缩写:PPI),又被称为像素密度,是一个表示打印图像或显示器单位长度上像素数量的指数 (并非单位面积的像素量)。一般用来计量电脑显示器,电视机和手持电子设备屏幕的精细程度。通常情况下,每英寸像素值越高,屏幕能显示的图像也越精细。5PPI表示每英寸有5个像素,500PPI表示每英寸有500个像素。
-
屏幕分辨率:也叫做像素分辨率,常用屏幕上每英寸长度内包含的像素数量来表达,即,Pixel per Inch,因此简写为 PPI
(或 DPI),一般地图的默认屏幕分辨率是96。有的地方也用像素大小(pixel size)来描述屏幕的可分辨率,如 WMTS 标准中的0.28mm(标准化渲染像素大小)。💡 前文中对于0.28mm的由来做了描述:0.28 毫米是 2005 年普通显示器的实际像素尺寸。其对应的DPI为:25.4/0.28=90.7142857142857
ps:自 20 世纪 80 年代以来,Microsoft Windows 操作系统已将其默认的标准显示每英寸像素 (PPI) 设置为 96。该值(即像素大小)的结果约为每像素 0.264 mm,该值的来源:25.4/96=0.26458333333333334毫米,即约为0.264 mm
💡 PPI和DPI都是描述分辨率(屏幕分辨率、空间分辨率是其中的分类)的单位。不过PPI和DPI经常都会出现混用现象。但是他们所用的领域也存在区别。从技术角度说,“像素(pixel)”只存在于电脑显示领域,而“点(dot)”只出现于打印或印刷领域。所以,私以为,除地图打印的场景外,为了在屏幕渲染的地图分辨率应该使用PPI而不是DPI,毕竟此处强调的是屏幕分辨率。🤔
-
Resolution(地图分辨率):在 GIS 领域所提到的地图分辨率(Resolution),也称地面分辨率(Ground Resolution)或空间分辨率(Spatial Resolution),表示屏幕上一个像素(pixel)所代表的实际地面距离,也就是一个像素代表多少地图单位(地图单位/像素),地图单位取决于数据所使用的空间参考(是米还是度)。
💡 即指代地图在图像中每一像素下,表示的地理空间距离(distance per pixel)。可以是每像素多少米(平面),也可以是每像素多少度(当前主要表示经纬度直投的方式下的度量)
在此处,是一个具体的概念与单位的结合体。本质上就是分辨率,与PPI、DPI并无太大区别,只不过前两者以英寸为单位,以单位内像素数量为度量;此处的dpp以像素为单位,以单位内地理空间距离为度量。都是用于分辨率的表达。
是不是可以写作:Spatial distance per pixel(sdpp)、Distance per pixel(dpp)、Groud distance per pixel(gdpp) 也未可知🙄
-
Scale(比例尺):地图比例尺(scale)是指地图上距离与地面实际距离的比例(也就是地图上1厘米表示实际的地面距离,厘米作为单位)。例如当实际距离为1,000米,而在地图上的距离为1厘米时,则称这一地区的比例尺是1:100,000。一般将比例尺为1:1至1:600000的地图称为大比例尺地图,1:600000至1:2,000,000的地图称为中比例尺地图,1:2000000至1:∞的地图称为小比例尺地图。在计算地图比例尺的时候,通常用到地图分辨率和屏幕分辨率这两个参数。
比例尺是通过地面分辨率(Resolution)和屏幕分辨率(PPI)由如下公式来定义的:
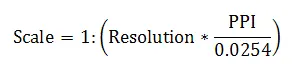
- Resolution:即地图分辨率、地面分辨率,是指一个像素(pixel)所代表的实际地面距离(米,此处需要将单位转换为米进行计算)
- PPI:屏幕分辨率度量单位,是指屏幕上每英寸长度内包含的像素数量,目前基本上都是96
- 0.0254(m/inch)是指米与英寸的单位转换
可以用这个公式,对比例尺(scale)和分辨率(resolution)进行换算。
其中,WMTS 1.0.0标准中没有规定屏幕分辨率(pixel/inch),而是用像元大小(0.28mm=0.00028m)来界定的,二者的换算关系是:
ppi = 1 inch/(pixelSize(m)/0.0254)所以,对于 WMTS 1.0.0接口(也是GeoWebCache的默认状态),PPI为:
1 inch/(0.00028m/0.0254(m/inch))=0.0254/0.00028=90.71428571428572≈90.714💡 如果遇到使用的空间参考单位为度,比如使用经纬度直投时,那么就需要将度转换为米进行计算。该值与OGC中的metersPerUnit对应,计算方式为:赤道处周长/360.0。CGCS2000|WGS84的转换参数为:
6378137.0 * 2.0 * Math.PI / 360.0=111319.49079327358 米/度此段内容参考自超图的比例尺与分辨率一文,且与地理信息公共服务平台电子地图数据规范中数据中显示比例尺计算公式进行比较,确定一致。


格网划分
准确说,应该是规则格网划分。也就是在特定的比例(尺度下)对给定的范围,按照指定的瓦片规格进行规则划分,形成平铺网格,即瓦片矩阵(TileMatrix),通常以矩阵的宽和高来表示。而瓦片矩阵集(TileMatrixSet)是由一组以不同比例定义的切片矩阵组成,也就是说,需要先有一组比例集合(尺度分级集合)。
ps: 当然也可以自行从给定的范围进行计算。
在此,可以直接使用地理信息公共服务平台电子地图数据规范中地图分级或者是天地图的分级,就类似于OGC中提到的Well-Known Scale Set。
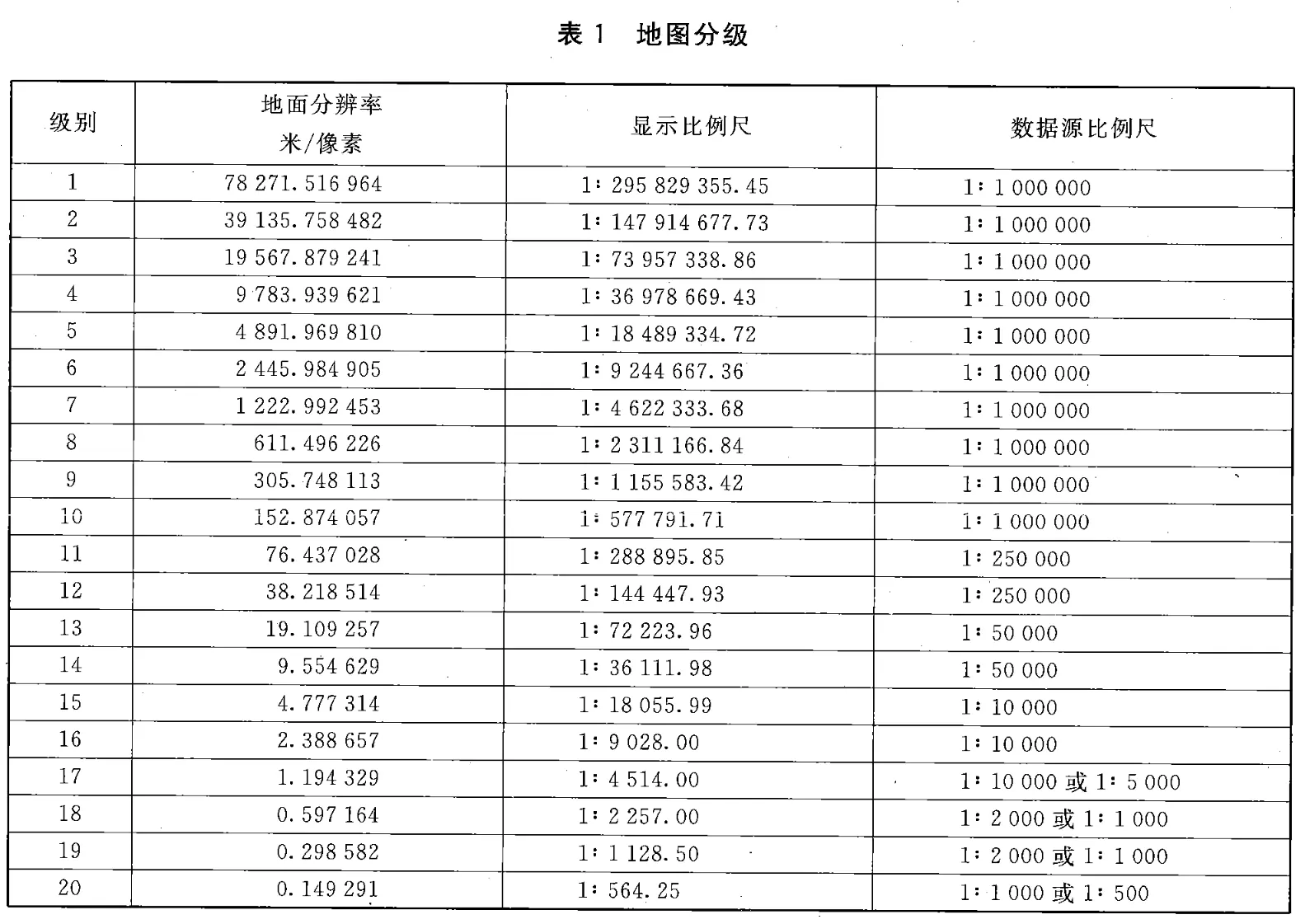
欲要继续进行格网划分,在确定比例分级(尺度分级)的基础上,还需要确定如下几个参数:
- crs:坐标参考系统,即格网所使用的空间参考
- extent:格网范围,通常是所用参考系统的最大范围
- PPI:一般默认使用96,不过OGC使用90.71428571428572
- Tile Size:一般默认使用256 x 256,像素为单位
- CornerOfOrigin:原点角,通常为左上角,TMS惯用的则是左下角
目前国内常用的大范围瓦片矩阵集(通用瓦片矩阵集)有两种,分别是基于Web墨卡托投影、和基于CGCS2000大地坐标系等间隔直投(经纬度直投)。这里,我们先看一下基于Web墨卡托投影的瓦片矩阵集的格网划分过程(也就是TileMatrixSet的构建过程),参数则取上述的默认值或通用值。
基于Web墨卡托投影的瓦片矩阵集的格网划分
墨卡托投影,是等角正轴圆柱投影,由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网(地球椭球面上的经纬线)投影于圆柱面上,并沿圆柱母线切开展为平面后,即得本投影。从其定义可知,墨卡托投影具有两种形态,分别是切圆柱投影及割圆柱投影,其中,最早也是最常用的是切圆柱投影(像我们平时所述的墨卡托投影基本上都是指代等角正轴切圆柱投影)。
💡 墨卡托投影(等角正轴切圆柱投影)以赤道作为标准纬线,以首子午线(本初子午线)为中央经线,其交点为坐标原点。也就是说,投影展开的母线对应椭球面的180°经线(又称为逆子午线或对向子午线(antimeridian),是本初子午线向东或向西180度的经线,既为东经180°,又为西经180°)
Web 墨卡托投影是墨卡托投影(等角正轴切圆柱投影)的一种变体,同时也是 web 地图和在线服务的事实标准。对于小比例尺地图,它与标准的墨卡托用的公式一样。但Web墨卡托在所有比例尺下都使用球面公式,但大比例尺的墨卡托地图通常使用投影的椭球面形式。这种差异在全球比例尺下是察觉不到的,但会导致局部地区的地图稍微偏离同一比例尺的真正的椭球面墨卡托地图。 虽然Web墨卡托的公式是墨卡托的球面形式,但地理坐标必须得以WGS 84椭球面基准获得。此差异会导致投影略微不符合正形投影。
💡 Web墨卡托投影在技术实现上为了简化计算,假设地球是一个球体,而非严格的椭球体。这使得它既不是严格的椭球面投影,也不是严格的球面投影,EPSG的定义说这个投影“使用椭球坐标系的球面演化”。它是建立在地球表面的WGS84椭球面模型定义的地理坐标上的,但在投影的时候却仿佛坐标是定义在球面上的。
Web墨卡托投影的范围:[-20037508.3427892, -20037508.3427892, 20037508.3427892, 20037508.3427892],经投影后所得投影面的投影坐标系如下图所示:
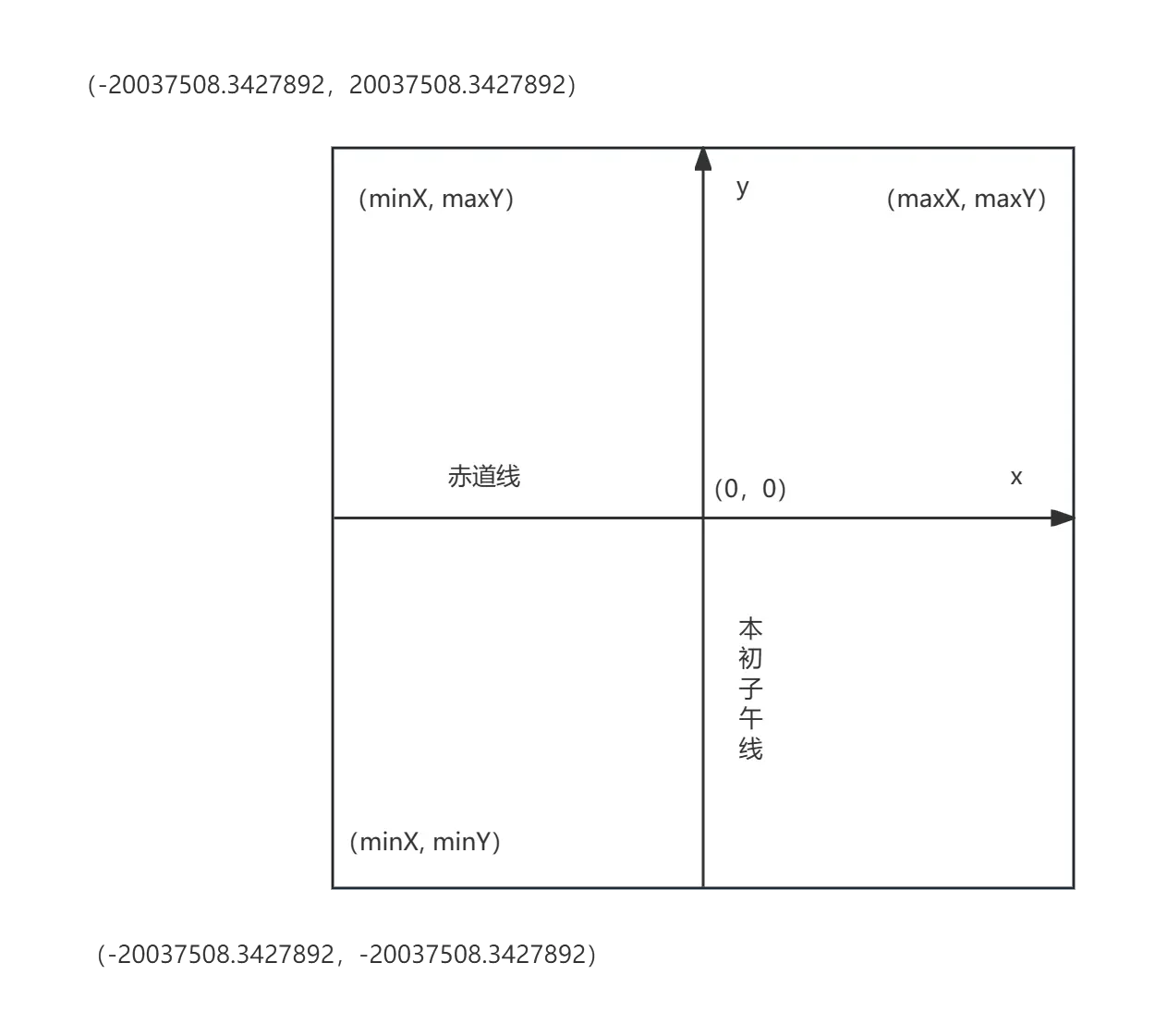
💡 Web墨卡托投影应是基于墨卡托(等角正轴切圆柱投影)的变体,其同样以赤道为标准纬线,本初子午线为中央经线,两者交点为坐标原点,向东和向北为正。
此时需要再次放出TileMatrixSet的示意图了,因为要开始进行格网划分,并构建瓦片矩阵集了,有图好理解些。
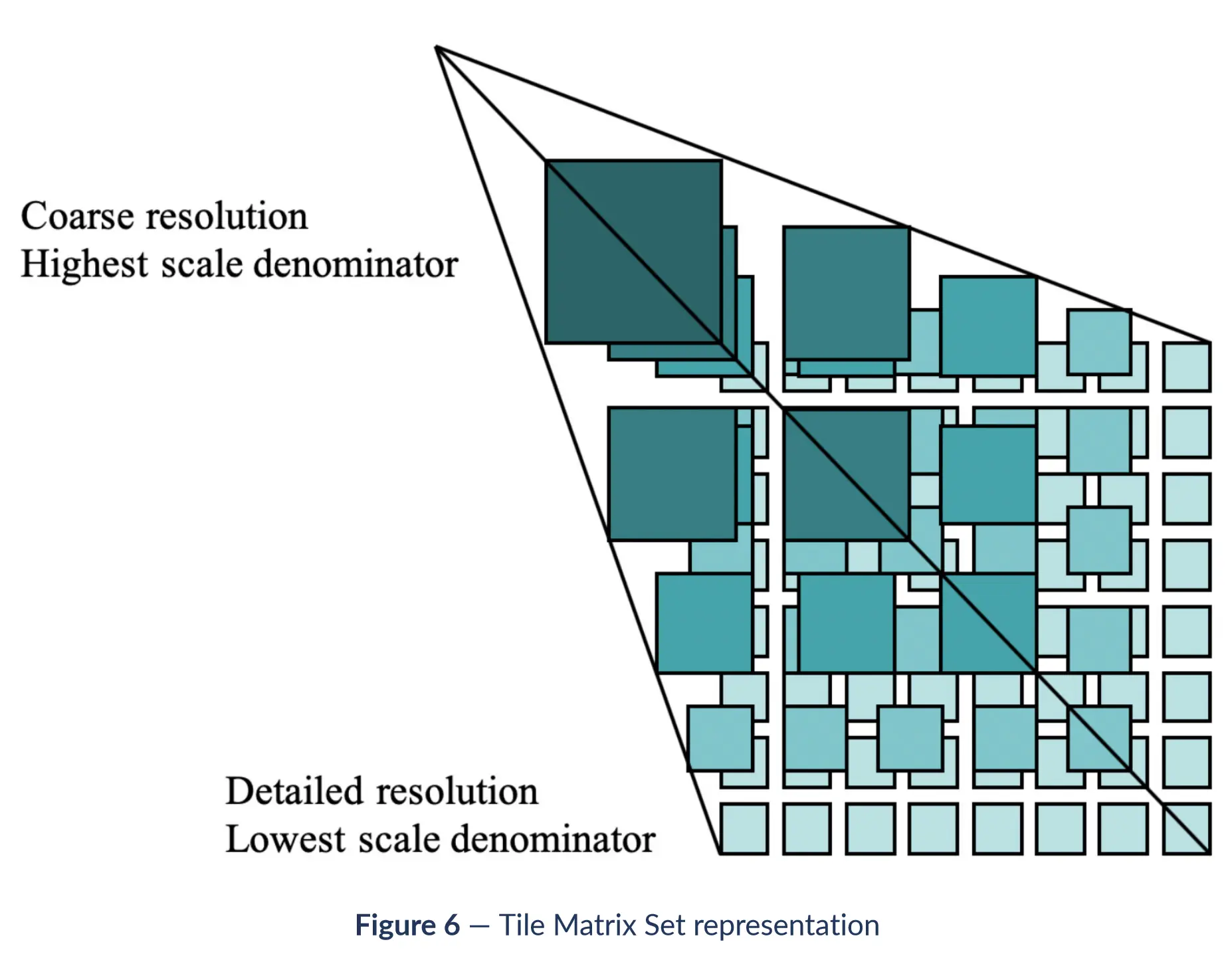
再次确定一下参数值:
- crs:3857|900913
- extent:[-20037508.3427892, -20037508.3427892, 20037508.3427892, 20037508.3427892]
- PPI:96
- Tile Size:256 x 256
- CornerOfOrigin:左上角
- Scale Set:天地图,因上述地图分级缺少矩阵数量,所以改用天地图,不过比例都是一致的。

如上图所示,天地图的分级是从1级开始的,1级以2x2的分布共计4张瓦片。从此处看其缺少0级。我们可以补充一下,并可进行核对。目前地图比例分级通常都采用2的倍率进行切片,也就是说当前级比例是下一级的2倍。第0级用一张瓦片(256x256)表示全部范围,那么在此可以计算:
// 0级的分辨率为(Extent Width / tile size)
(20037508.3427892 * 2)/256=156543.03392804062
// 0级比例尺为(根据上述提供的比例尺计算公式进行计算)
1: (156543.03392804062 * 96/0.0254)=1: 5.916587109091299E8
// 核对一下1级的分辨率和比例尺
156543.03392804062/2=78271.51696402031
5.916587109091299E8/2=2.958293554545649E8
这里可以发现我们算出来的1级的比例尺的最后两位小数与天地图的有点差别(其实使用上应没有什么问题了),原因是因为我们使用的范围其实是相对不精确的。接下来,我们使用WGS84椭球体的赤道圈作为范围来计算(避免小数位保留问题导致计算不一致问题)
// 0级的分辨率为
(20037508.3427892 * 2)/256=156543.03392804097
// 0级比例尺为
1: (((6378137.0 * 2.0 * Math.PI)/256) * 96/0.0254)=1: 5.916587109091312E8
// 核对一下1级的分辨率和比例尺
156543.03392804097/2=78271.51696402048
5.916587109091312E8/2=2.958293554545656E8
这一次发现,1级的比例尺与天地图的完全一致了。之所以从0级开始说明,这是因为当没有给定比例分级的时候,可以自行基于给定的范围和2的倍率的方式计算分级。当给定分级,则可直接基于分级做后续计算。其中重点,就是计算每一个分级下,矩阵的宽度和高度(以此来作为矩阵描述)。我们在此基于天地图的比例尺分级进行1-5级的瓦片矩阵计算,并进行对比验证(分辨率的计算方式由比例尺计算公式反推)。
// Extent Width: (6378137.0 * 2.0 * Math.PI)=4.007501668557849E7
// 1级比例尺:2.958293554545656E8
// 1级矩阵 2x2
resolution=(2.958293554545656E8*0.0254)/96=78271.51696402048
// 范围的宽 / 瓦片对应的宽
matrixWidth=4.007501668557849E7/(256*78271.51696402048)=2
// 范围的高(Web墨卡托投影平面是正方形, 所以宽高一致) / 瓦片对应的高
matrixHigh=4.007501668557849E7/(256*78271.51696402048)=2
// 2级比例尺:1.479146777272828E8
// 2级矩阵 4x4
resolution=(1.479146777272828E8*0.0254)/96=39135.75848201024
// 范围的宽 / 瓦片对应的宽
matrixWidth=4.007501668557849E7/(256*39135.75848201024)=4
// 范围的高 / 瓦片对应的高
matrixHigh=4.007501668557849E7/(256*39135.75848201024)=4
// 3级比例尺:7.39573388636414E7
// 3级矩阵 8x8
resolution=(7.39573388636414E7*0.0254)/96=19567.87924100512
// 范围的宽 / 瓦片对应的宽
matrixWidth=4.007501668557849E7/(256*19567.87924100512)=8
// 范围的高 / 瓦片对应的高
matrixHigh=4.007501668557849E7/(256*19567.87924100512)=8
// 4级比例尺:3.69786694318207E7
// 4级矩阵 16x16
resolution=(3.69786694318207E7*0.0254)/96=9783.93962050256
// 范围的宽 / 瓦片对应的宽
matrixWidth=4.007501668557849E7/(256*9783.93962050256)=16
// 范围的高 / 瓦片对应的高
matrixHigh=4.007501668557849E7/(256*9783.93962050256)=16
// 5级比例尺:1.848933471591035E7
// 5级矩阵 32x32
resolution=(1.848933471591035E7*0.0254)/96=4891.96981025128
// 范围的宽 / 瓦片对应的宽
matrixWidth=4.007501668557849E7/(256*4891.96981025128)=32
// 范围的高 / 瓦片对应的高
matrixHigh=4.007501668557849E7/(256*4891.96981025128)=32
经过再次对比,可确定此计算与天地图以及电子地图规范中的地图分级数据一致。且已经完成格网划分动作,是的,其实就是这么简单。确定好参数后,直接进行矩阵构建(格网划分)就好了(矩阵宽,高计算)。
如果你需要从范围去计算比例分级的话,需要注意的,本次给定的范围是比较特殊的,是相当规整的,因为Web墨卡托的投影面结果是一个正方形的平面区域。所以对于方形瓦片来说,其在正方形的区域下横纵方向的分辨率是一致的。如果给定的区域是长方形或者其他的形状,则可能需要进行一定的范围调整,以保证方形瓦片在横纵方向上的分辨率是统一的,同时矩阵在横纵方向上数量是整数(整除的)。
基于CGCS2000经纬度投影的瓦片矩阵集的格网划分
经纬度等间隔直投:英文叫法是Platte Carre projection,是等距矩形投影(Equirectangular projection)基准点纬度取0°(赤道)时的特殊情况。它的特点是相同的经纬度间隔在屏幕上的间距相等,没有复杂的坐标变换。我们可简单的理解为,在笛卡尔坐标系中,将赤道作为X轴,子午线(本初子午线)作为Y轴,然后把本来应该在南北两极相交的经线一根一根屡直了,成为了互相平行的经线,而每条纬线的长度也在这个过程中都变为与赤道等长。
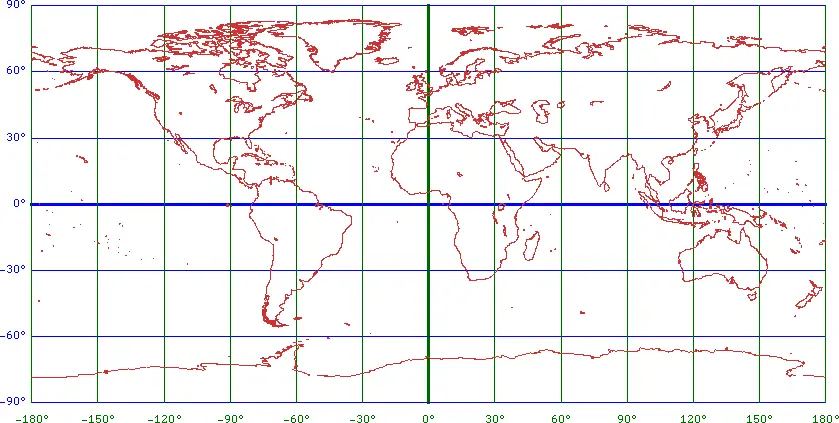
再次确定一下参数值:
- crs:4490
- extent:[-180.0 -90.0, 180.0 90.0]
- PPI:96
- Tile Size:256 x 256
- CornerOfOrigin:左上角
- Scale Set:天地图。
在这里我们直接进行1-5级的瓦片矩阵计算验证,由于当前是投影使用经纬度单位,需要需要将默认的米转换为度:
// EPSG_4490_TO_METERS: 6378137.0 * 2.0 * Math.PI / 360.0=111319.49079327358
// 1级比例尺:2.958293554545656E8
// 1级矩阵 2x1
resolution=(2.958293554545656E8*0.0254/111319.49079327358)/96=0.703125
// 范围的宽 / 瓦片对应的宽
matrixWidth=360/(256*0.703125)=2
// 范围的高(Web墨卡托投影平面是正方形, 所以宽高一致) / 瓦片对应的高
matrixHigh=180/(256*0.703125)=1
// 2级比例尺:1.479146777272828E8
// 2级矩阵 4x2
resolution=(1.479146777272828E8*0.0254/111319.49079327358)/96=0.3515625
// 范围的宽 / 瓦片对应的宽
matrixWidth=360/(256*0.3515625)=4
// 范围的高 / 瓦片对应的高
matrixHigh=180/(256*0.3515625)=2
// 3级比例尺:7.39573388636414E7
// 3级矩阵 8x4
resolution=(7.39573388636414E7*0.0254/111319.49079327358)/96=0.17578125
// 范围的宽 / 瓦片对应的宽
matrixWidth=360/(256*0.17578125)=8
// 范围的高 / 瓦片对应的高
matrixHigh=180/(256*0.17578125)=4
// 4级比例尺:3.69786694318207E7
// 4级矩阵 16x8
resolution=(3.69786694318207E7*0.0254/111319.49079327358)/96=0.087890625
// 范围的宽 / 瓦片对应的宽
matrixWidth=360/(256*0.087890625)=16
// 范围的高 / 瓦片对应的高
matrixHigh=180/(256*0.087890625)=8
// 5级比例尺:1.848933471591035E7
// 5级矩阵 32x16
resolution=(1.848933471591035E7*0.0254/111319.49079327358)/96=0.0439453125
// 范围的宽 / 瓦片对应的宽
matrixWidth=360/(256*0.0439453125)=32
// 范围的高 / 瓦片对应的高
matrixHigh=180/(256*0.0439453125)=16
CGCS2000经纬度等间隔直投后所得投影平面就是一个长方形,宽为360°,高为180°。假如此时要以范围进行比例分级计算的话,以256x256瓦片来计算单张瓦片覆盖完整区域的情况(即0级,矩阵1x1的情况)会发现横纵方向上的分辨率不一致,且横向恰好是纵向的2倍。在GeoWebCache中,其默认以小边(即分辨率较低的一边)为主,通过一定规则对范围进行调整(即寻找一个同时适合横纵方向的分辨率,而后基于此计算新的范围)。对于[-180,-90,180,90]这个范围,最终直接以纵向的分辨率(0.703125)为主进行范围调整,因横向分辨率恰好是纵向的2倍,所以最终范围没有发生变化。
resX=360/256=1.40625
resY=180/256=0.703125
当然,GeoWebCache中不仅只有这一种构建TileMatrixSet的策略,以范围进行构建的更适合没有提供比例分级的情况,其它的还有给定基比例分母(分辨率或比例尺)的方式,或是给定完整的比例分级集合。
💡 再回顾一下上节附录中提到的4326瓦片矩阵集其0集是2x1,在这个TileMatrixSet中,标识符为“-1”的TileMatrix只有一个图块,有128行留空。因此,许多实施者不想提供这一级别(包括 INSPIRE 技术指南),而是更喜欢从仅用 2 个瓦片(一个用于负经度,一个用于正经度)表示世界的 TileMatrix 开始。
所以GeoWebCache以范围进行TileMatrixSet构建的程序中,其以小边为主必然会导致如CGCS2000(或WGS84)经纬度直投的方式不存在有单张瓦片覆盖全部区域的层级。
此段内容较为粗糙,主要以说明其计算原理为主。如果你对此部分内容感兴趣,可以去看一下GeoWebCache中GridSetFactory类的实现,或者是去看Geo Atlas中TileMatrixSetFactory类的实现(我加了部分中文注释 ☺️)
关于像素大小(Pixel Size)的影响
对于地图分辨率(Resolution)和比例尺(Scale)来说,其实像素大小(pixel size)影响的只有比例尺。所以即使是使用不同的像素大小构建的瓦片矩阵集,只要其地图分辨率是一致的,那么瓦片就可正确的叠加在一起。如下图所示,左侧是我在GeoServer(0.28mm)中配置的CGCS2000经纬度投影的瓦片矩阵集(Geo Atlas中4490同理进行配置),右下则为天地图(0.26458mm)的CGCS2000经纬度投影的瓦片矩阵集。
![]()
坐标转换(tile coordinates ↔ crs)
此处所提坐标转换即为描述如何将瓦片坐标系与其对应的空间坐标系进行相互转换。对于大地坐标系或投影坐标系肯定是熟悉的,这里对瓦片坐标系再次进行说明下。
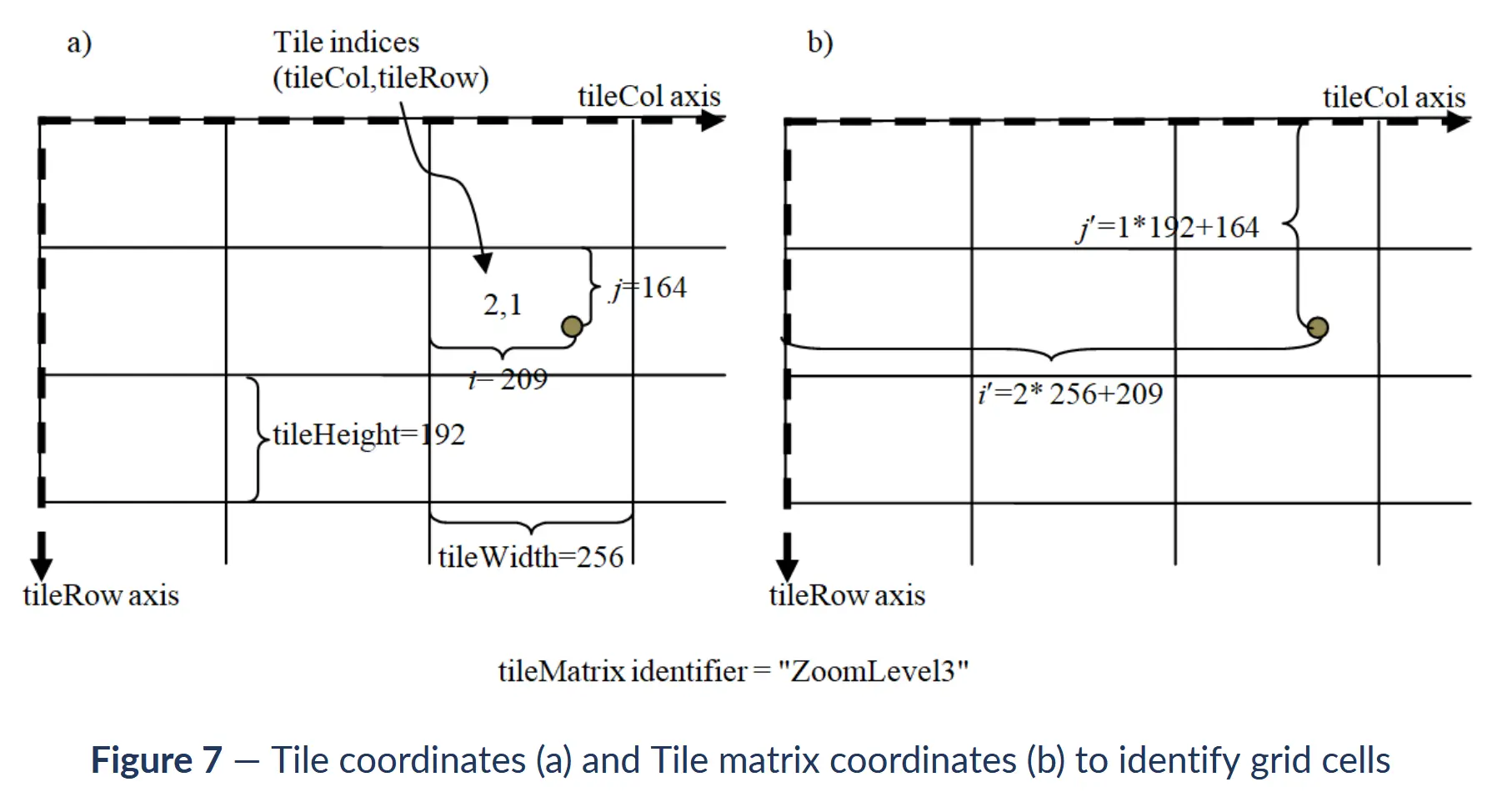
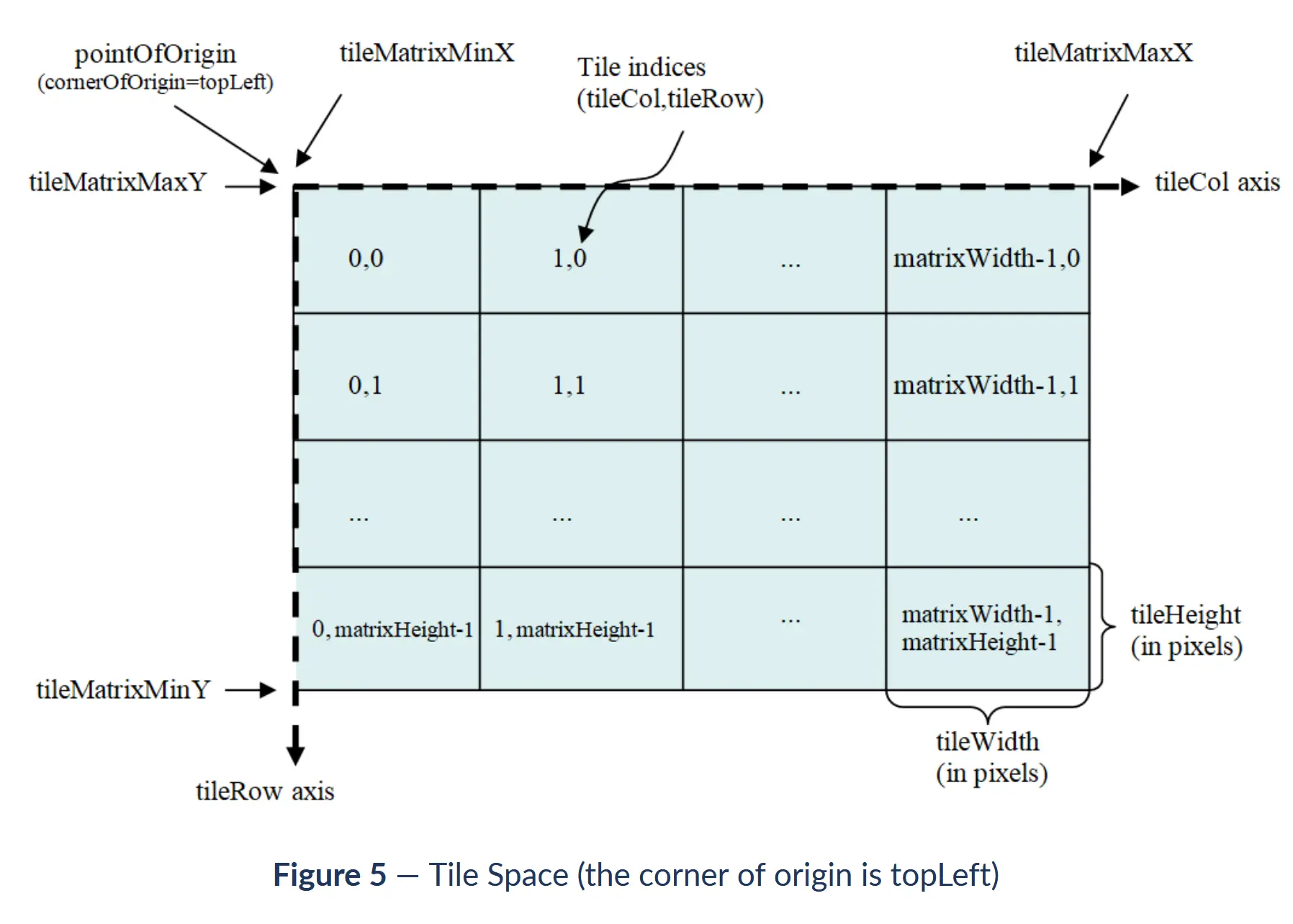
上图均为切片原点为左上角的瓦片矩阵集的瓦片坐标系,如果切片原点在左下角,那么tileCol 轴不变,而tileRow轴由下指向上,与当前图示的tileRow轴方向相反。瓦片坐标从0值开始,切片原点处的瓦片坐标为(0, 0)。
对于两种坐标的转换,其实上文附录部分也有做简要说明,不过仅仅只是伪代码,如今我们就直接看代码吧。
💡 注:以下所展示内容均指代切片原点在左上角的情况。
Tile Coordinates → Crs BBox
- 瓦片坐标
- tileRow,对应Y
- tileCol,对应X
- tileZoom,对应Z
瓦片坐标系转其对应的空间坐标系(即瓦片占据的空间范围)的逻辑其实很好理解。正如格网划分是需要基于某个投影坐标系下进行,划分的同时也是将投影空间转换为瓦片矩阵空间,现在只需要反向推算回去即可。也就是,需要计算出瓦片的左下角和右上角对应的投影坐标。
需要提供的参数:
- 切片原点方位以及投影坐标:如下表示的切片原点是左上角
- 每个层次的分辨率以及瓦片宽高
public BoundingBox boundsFromIndex(long[] tileIndex) {
final int tileZ = (int) tileIndex[2];
TileMatrix matrix = getMatrix(tileZ);
long tileX = tileIndex[0];
long tileY;
// 计算瓦片在横向上占据了多少地图单位,比如256在当前层级表示多少米或度
double width = matrix.getResolution() * (double) matrix.getTileWidth();
double height = matrix.getResolution() * (double) matrix.getTileHeight();
double[] tileOrigin = this.tileOrigin();
BoundingBox tileBounds;
// 此处假定传递的瓦片坐标属于google体系的瓦片坐标系,即原点在左上角
if (CornerOfOrigin.TOP_LEFT.equals(this.cornerOfOrigin)) {
tileY = tileIndex[1];
// (minx, miny, maxx, maxy)
tileBounds = new BoundingBox(tileOrigin[0] + width * (double) tileX,
tileOrigin[1] - height * (double) (tileY + 1L),
tileOrigin[0] + width * (double) (tileX + 1L),
tileOrigin[1] - height * (double) tileY);
} else {
throw new IllegalArgumentException("Unsupported corner of origin: " + this.cornerOfOrigin);
}
return tileBounds;
}
💡 值得注意的是,我在此表示BBox用的是左下角和右上角的方式。此种思考方式与切片原点在左上角的瓦片坐标系有些不太统一,总之有点别扭。或许当切片原点在左上角时,使用左上角与右下角表示BBox对于思考更友好些 也未可知啊 🙄
这难道就是OGC初始提倡使用左下角作为切片原点的理由吗?一方面左下角沿横纵方向都是逐渐增大,更符合人们的思考;另一方面,对于BBox的描述多使用左下角和右上角?🤨
Crs BBox → Tile Coordinates
上文附录提到的BBOX转瓦片坐标系,是获取到一系列的瓦片坐标系。也就是给定BBox,然后获取到对用的瓦片坐标范围。但是附录中并未提到关于比例层级的内容,不过逻辑是所有层级都是共用的。
那么在此基于GeoWebCache的实现,提供两类BBox → Tile Coordinates的转换方法。一类是获取与给定范围最接近的瓦片坐标系,另一类则是上文附录提到的一系列的瓦片坐标系。
ClosestIndex
此方法为获取与给定范围最接近的瓦片坐标系,其仅仅适用于将一个正确的瓦片的BBox转换为瓦片坐标,不适用于任意的BBox(即随意构造的BBox)。
// 首先是找到与给定的BBox最匹配的TileMatrix的索引,它遍历所有层级的瓦片矩阵,
// 计算每个层级的分辨率误差,并选择误差最小的层级。同时,它还检查分辨率的一致性,
// 确保与之前的最佳分辨率相差不超过10%。
protected long[] closestIndex(BoundingBox tileBounds) throws MatrixMismatchException {
double wRes = tileBounds.getWidth() / getMatrix(0).getTileWidth();
// 保存最小的分辨率误差,初始值为最大双精度值(无限大)
double bestError = Double.MAX_VALUE;
// 保存最佳的瓦片矩阵层级索引,初始值为-1
int bestLevel = -1;
// 保存最佳的分辨率,初始值为-1.0
double bestResolution = -1.0;
for (int i = 0; i < getNumLevels(); i++) {
TileMatrix grid = getMatrix(i);
double error = Math.abs(wRes - grid.getResolution());
if (error < bestError) {
bestError = error;
bestResolution = grid.getResolution();
bestLevel = i;
} else {
break;
}
}
if (Math.abs(wRes - bestResolution) > (0.1 * wRes)) {
throw new ResolutionMismatchException(wRes, bestResolution);
}
return closestIndex(bestLevel, tileBounds);
}
protected long[] closestIndex(int level, BoundingBox tileBounds)
throws MatrixAlignmentMismatchException {
TileMatrix grid = getMatrix(level);
double width = grid.getResolution() * grid.getTileWidth();
double height = grid.getResolution() * grid.getTileHeight();
double x = (tileBounds.getMinX() - tileOrigin()[0]) / width;
double y = (tileOrigin()[1] - tileBounds.getMaxY()) / height;
long posX = Math.round(x);
long posY = Math.round(y);
if (Math.abs(x - posX) > 0.1 || Math.abs(y - posY) > 0.1) {
throw new MatrixAlignmentMismatchException(x, posX, y, posY);
}
long[] ret = {posX, posY, level};
return ret;
}
ClosestRectangle
此方法对应上文附录提到的将给定BBox转换为对应的一系列的瓦片坐标系。其同样是先找到与给定的BBox最匹配的TileMatrix的索引,而后计算对应索引层级下BBox对应的瓦片坐标范围。该方法适用于任意范围。
public long[] closestRectangle(BoundingBox rectangleBounds) {
double rectWidth = rectangleBounds.getWidth();
double rectHeight = rectangleBounds.getHeight();
double bestError = Double.MAX_VALUE;
int bestLevel = -1;
// Now we loop over the resolutions until
for (int i = 0; i < getNumLevels(); i++) {
TileMatrix grid = getMatrix(i);
double countX = rectWidth / (grid.getResolution() * grid.getTileWidth());
double countY = rectHeight / (grid.getResolution() * grid.getTileHeight());
double error =
Math.abs(countX - Math.round(countX)) + Math.abs(countY - Math.round(countY));
if (error < bestError) {
bestError = error;
bestLevel = i;
} else if (error >= bestError) {
break;
}
}
return closestRectangle(bestLevel, rectangleBounds);
}
protected long[] closestRectangle(int level, BoundingBox rectangeBounds) {
TileMatrix grid = getMatrix(level);
double width = grid.getResolution() * grid.getTileWidth();
double height = grid.getResolution() * grid.getTileHeight();
long minX = (long) Math.floor((rectangeBounds.getMinX() - tileOrigin()[0]) / width);
long minY = (long) Math.floor((tileOrigin()[1] - rectangeBounds.getMaxY()) / height);
long maxX = (long) Math.ceil(((rectangeBounds.getMaxX() - tileOrigin()[0]) / width));
long maxY = (long) Math.ceil(((tileOrigin()[1] - rectangeBounds.getMinY()) / height));
// We substract one, since that's the tile at that position
long[] ret = {minX, minY, maxX - 1, maxY - 1, level};
return ret;
}
TileMatrixSet in Geo Atlas
其实在Geo Atlas,用于构建矢量切片服务的Java基础库一文中也曾提到,Pyramid、IO(in Library)、Tile Cache模块均来自GeoWebCache,是对其进行了拆解和少量变更。TileMatrixSet就是来自于GeoWebCache的GridSet,在此处对其进行了少量修改:
-
切片原点修改为左上角(GeoWebCache默认还是使用左下角作为切片原点,不过也支持配置为左上角)
-
将构造GridSet的SRS变更为的CRS(不再割裂)
-
默认提供3857&4490(其实3857就是900913,只不过GeoTools原生并没有提供900913的坐标系声明;此处4490是遵循天地图CGCS2000经纬度等间隔直投的尺度分级构建,包含0级)
TileMatrixSet WORLD_EPSG_3857 = TileMatrixSetFactory.createTileMatrixSet( projectedName, CRS.decode("EPSG:3857", true), BoundingBox.WORLD3857, CornerOfOrigin.TOP_LEFT, TileMatrixSetFactory.DEFAULT_LEVELS, null, TileMatrixSetFactory.DEFAULT_PIXEL_SIZE_METER, 256, 256, false); TileMatrixSet WORLD_EPSG_4490 = TileMatrixSetFactory.createTileMatrixSet( projectedName, CRS.decode("EPSG:4490", true), BoundingBox.WORLD4490, CornerOfOrigin.TOP_LEFT, 1.40625d, // 天地图经纬度投影0级的分辨率 TileMatrixSetFactory.DEFAULT_LEVELS, TileMatrixSetFactory.EPSG_4326_TO_METERS, TileMatrixSetFactory.CGCS2000_PIXEL_SIZE_METER, 256, 256, false); -
命名变更,将GridSet变更为TileMatrixSet,Grid变更为TileMatrix。理由是:更符合瓦片矩阵的命名,同时OGC中也是如此命名的。
小结
下篇尝试着对TileMatrixSet的相关计算原理进行探讨说明,文中先后描述了TileMatrixSet在GeoWebCache及Geo Atlas中的实现,同时结合天地图提供的两种投影(Web墨卡托以及CGCS2000经纬度等间隔直投)下的瓦片矩阵集进行计算验证。整体看来,感觉还是有些混乱,计算原理部分的说明不够清晰,未达成心中想要的标准(布局合理、前后连贯、逻辑分明、层层递进、朗朗上口,也未可知啊 😒),再接再厉吧! 🙄
个人理解始终有限,如有存在偏颇的方法,还希望大家多多指教 😬🤝!